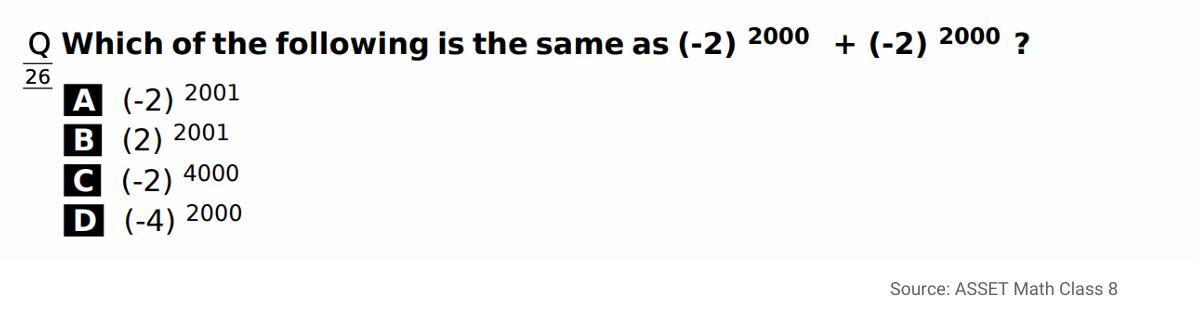Learning
Edition 06 | June 2025
From Learning Data to Classroom Instruction
Explore how data-driven insights can transform teaching by addressing
misconceptions and fostering deeper understanding.
The picture shows a mathematical question
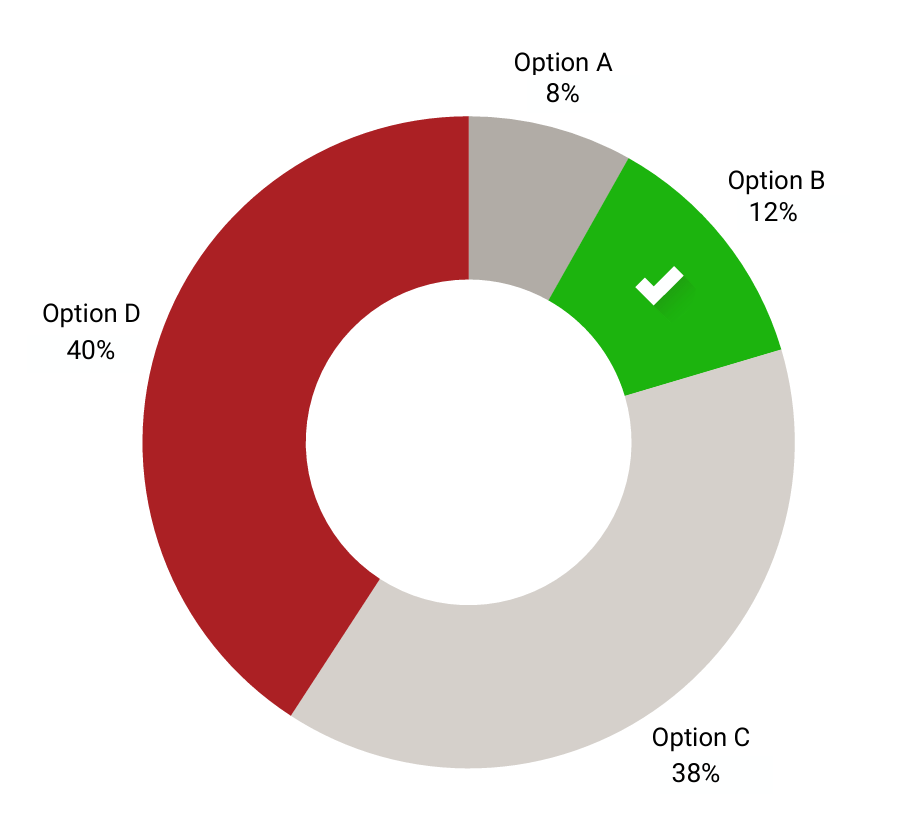
Correct answer: Option B
Most Common wrong answer: Option C and D
National Performance
What is the Question Testing?
This item checks whether learners understand and correctly apply the index laws when the bases
are identical and the base itself is negative. They must recognise that an even exponent makes
(−2)
What is the Most Common Wrong Answer and Possible Misconception?
- Most Common Wrong Answer: Option C (38%) and D (40%)
Distractor Explanation:
Students choosing option D might have incorrectly generalised the rules by adding the bases when
the exponents are the same. Those who selected option C may have mistakenly added the
exponents.
Both the incorrect choices show the surface level memory of ‘add something’ without grasping what may be added. Others ignore that an even exponent removes the negative sign.
Both the incorrect choices show the surface level memory of ‘add something’ without grasping what may be added. Others ignore that an even exponent removes the negative sign.
What Will Happen if Children Do Not Develop This Concept Adequately?
Conceptual Confusion in Algebra:
Students who misunderstand this will face difficulties in simplifying expressions, solving exponential equations, and understanding logarithmic functions. They may continue to confuse addition and multiplication of powers, which will hurt them in higher-level math (e.g., algebra, calculus, physics).
Long-Term Learning Gaps:
Without conceptual clarity, these errors can compound over time, leading to persistent mathematical anxiety, poor problem-solving skills, and low confidence in algebra-related topics.
Students who misunderstand this will face difficulties in simplifying expressions, solving exponential equations, and understanding logarithmic functions. They may continue to confuse addition and multiplication of powers, which will hurt them in higher-level math (e.g., algebra, calculus, physics).
Long-Term Learning Gaps:
Without conceptual clarity, these errors can compound over time, leading to persistent mathematical anxiety, poor problem-solving skills, and low confidence in algebra-related topics.
How Should I Remediate This in My Class?
Use Visual Analogies:
Build Number Sense:
- Show that just like 3 + 3 = 2 × 3, similarly x + x = 2x and so a2 + an = 2an
- Use base-ten blocks or repeated addition with powers to show conceptual grounding.
- Teach the difference between:
- Adding powers: an + an = 2a n
- Multiplying powers: an × am =a(n+m)
- Powers of powers: (an)m=an*m
Build Number Sense:
- Encourage logical checking: Is (-2)2000 + (-2)2000=(-4)2000?
Why not? What does it imply?
Enjoyed the read? Spread the word
Interested in being featured in our newsletter?
Check out the latest edition here.
